Training Quantization with Outlier Suppression in Training Time
Handling activation outlier in Transformer model is crucial to minimizing quantization error. In this blogpost, we explore simpler W8A8 training quantization without any explicit activation outlier suppression schemes.
Introduction
Training large language models (LLMs) has become increasingly expensive due to their growing size. To reduce the training cost, low-precision training has been proposed. This involves using lower-precision floating-point (FP) formats or quantization techniques, which can leverage hardware acceleration by performing matrix multiplications in integer formats. However, quantization introduces quantization errors, leading to instability and degraded accuracy during training.
One of major reason of quantization error is Activation Outliers, a common phenomenon in Transformer architectures
Previous studies have proposed specialized training techniques to reduce or eliminate activation outliers. For example,
In contrast, we explore a simpler training quantization technique using Clipped Softmax and Gated Attention, which is the methods that suppress activation outliers during training
To the best of our knowledge, there has been no prior work that simultaneously applies training quantization while actively preventing the emergence of outliers during training itself.
Preliminaries
Activation Outlier
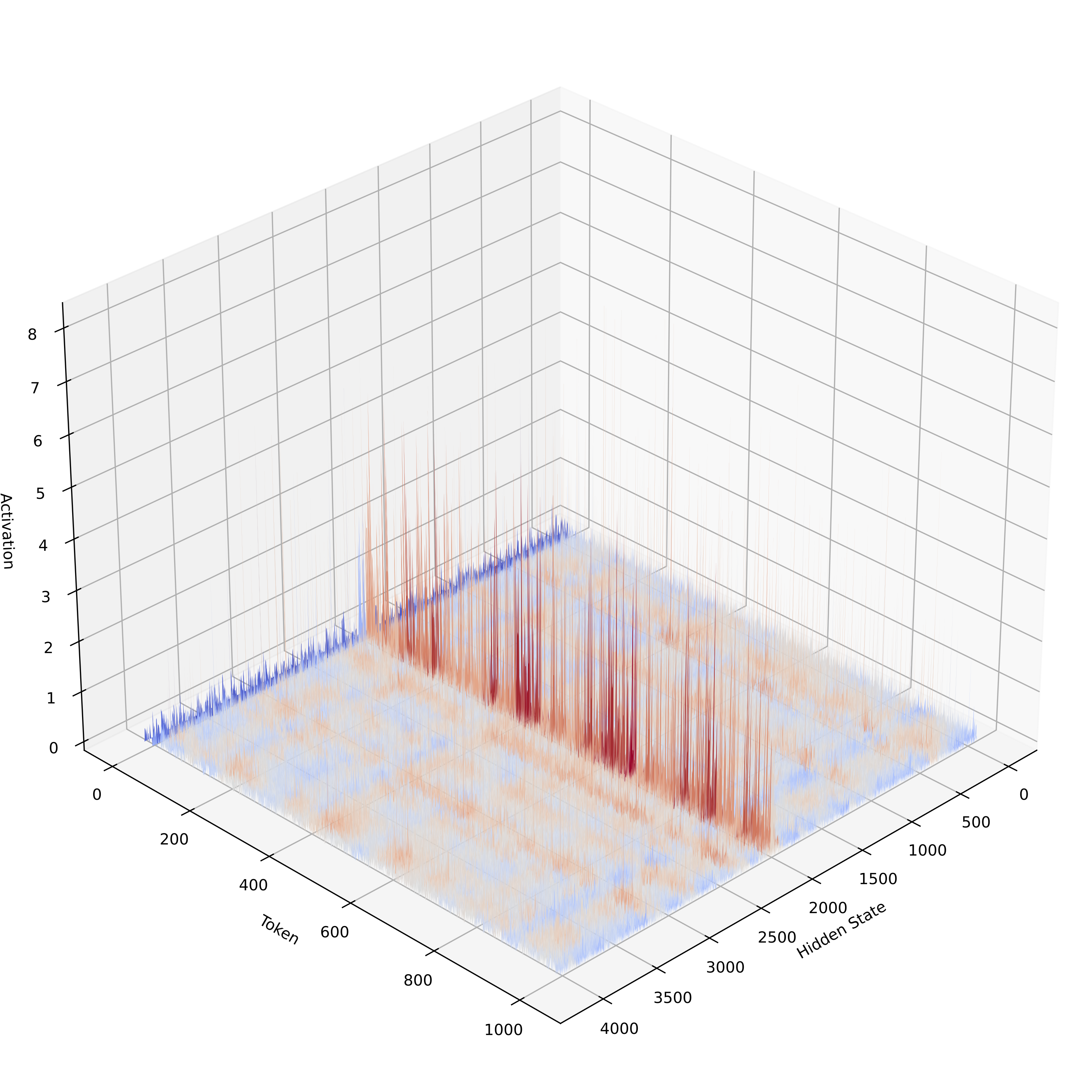
Activation outliers commonly emerge during the training process of Transformer models. Figure 1 visualizes the presence of activation outliers in a Transformer, where it is evident that these outliers appear in a channel-wise manner. Such outliers pose challenges for activation quantization, as they distort the value distribution within each channel. As a result, performing quantization, handling outlier values is crucial for minimizing quantization error.
Training Quantization
Training quantization is a technique that accelerates model training by converting data formats to integers during both the forward and backward passes. This reduces memory load/store overhead and enables efficient integer-based matrix multiplications. However, applying naive quantization to Transformer models in training is problematic due to the presence of activation outliers. These outliers make it difficult to quantize both outlier and non-outlier values accurately, leading to degraded training performance (Figure 2).
To address this issue, previous works have proposed various solutions. For example,
In contrast, we take a different approach by suppressing the formation of activation outliers during training itself. This enables accurate training-time quantization without requiring complex transformations like the Hadamard matrix.
How to Mitigate Activation Outlier in Training Time?
Quantizable Transformer paper
To address this issue,
Clipped Softmax
The clipped softmax is defined as follows:
\[\text{cilpped_softmax}(\mathbf{x};\zeta,\gamma) = \nonumber \text{clip}((\zeta-\gamma)\cdot\text{softmax}(\mathbf{x})+\gamma,0,1).\]where $\mathbf{x}$ is the input vector, and $\zeta \ge 1$ and $\gamma \le 0$ are stretch factors. This function clips the softmax output: values greater than $\frac{1 - \gamma}{\zeta - \gamma}$ are clipped to 1, and values smaller than $\frac{-\gamma}{\zeta - \gamma}$ are clipped to 0. With this modified function, we can ensure that certain softmax outputs become exactly 0. As a result, the activation values of no-op tokens no longer need to be excessively large to produce a near-zero softmax value, thereby preventing the occurrence of activation outliers.
Gated Attention
The gated attention is defined as follows:
\[\text{gated_attention}(\mathbf{x}) = \nonumber \text{sigmoid}(\mathbf{G}(\mathbf{x}))\odot\text{softmax}\left(\frac{\mathbf{Q}(\mathbf{x})\mathbf{K}(\mathbf{x})^T}{\sqrt{d_{head}}}\right)\mathbf{V}(\mathbf{x}).\]where $\mathbf{G}(\mathbf{x})$ is the gate, and $\mathbf{Q}(\mathbf{x})$, $\mathbf{K}(\mathbf{x})$, and $\mathbf{V}(\mathbf{x})$ are the query, key, and value of the attention head, respectively. $d_{\text{head}}$ denotes the dimensionality of the attention head. The gate plays the role of selecting which tokens should be updated. If the gate value is close to 0, the attention head will avoid updating the corresponding tokens. Similar to clipped softmax, the activation values of no-op tokens do not need to be excessively large, since the gate prevents the attention head from updating those tokens.
Clipped Softmax and Gated Attention are Effectively Mitigate Activation Outlier
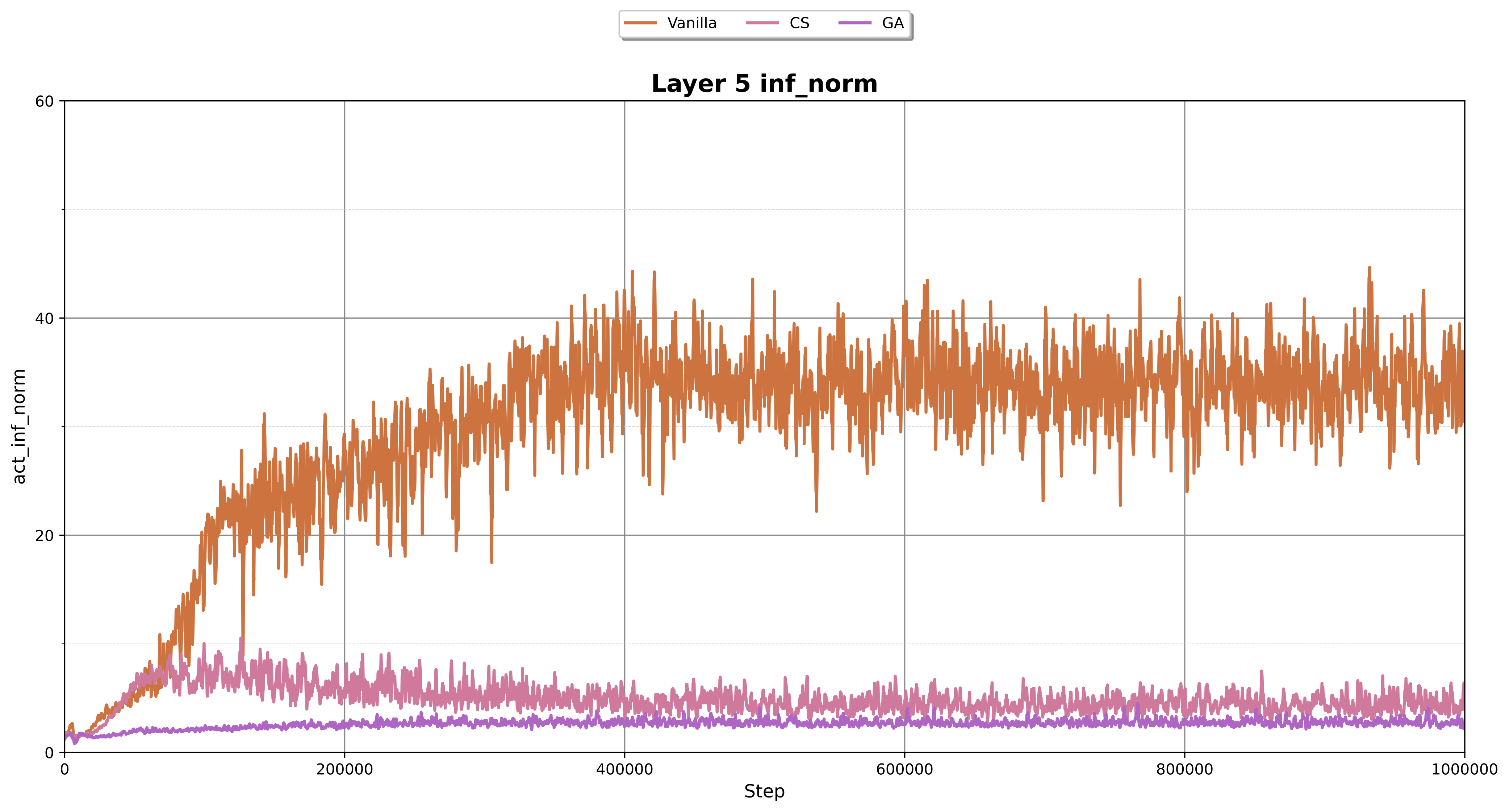
To observe the effect of clipped softmax and gated attention on activation magnitudes, we pre-trained a BERT-base model (detailed in the Experiment Setup section below). Figure 3 presents the \(\|X\|_{\infty}\) at each training step, where $X$ denotes the input activation to a BERT layer 5. The models incorporating clipped softmax and gated attention consistently exhibit significantly lower \(\|X\|_{\infty}\) values throughout training, whereas the original BERT model shows substantially higher values. These results demonstrate that clipped softmax and gated attention effectively suppress activation outliers during training.
Can We Apply Naive Training Quantization by Mitigating Activation Outlier?
This raises an interesting question: If activation outliers can be suppressed during training, can we then apply naive quantization during training without incurring significant errors? As shown in Figure 3, both clipped softmax and gated attention reduce the maximum activation norm, indicating fewer outliers. Based on this observation, we hypothesized that training quantization could be applied without additional operations for outlier suppression.
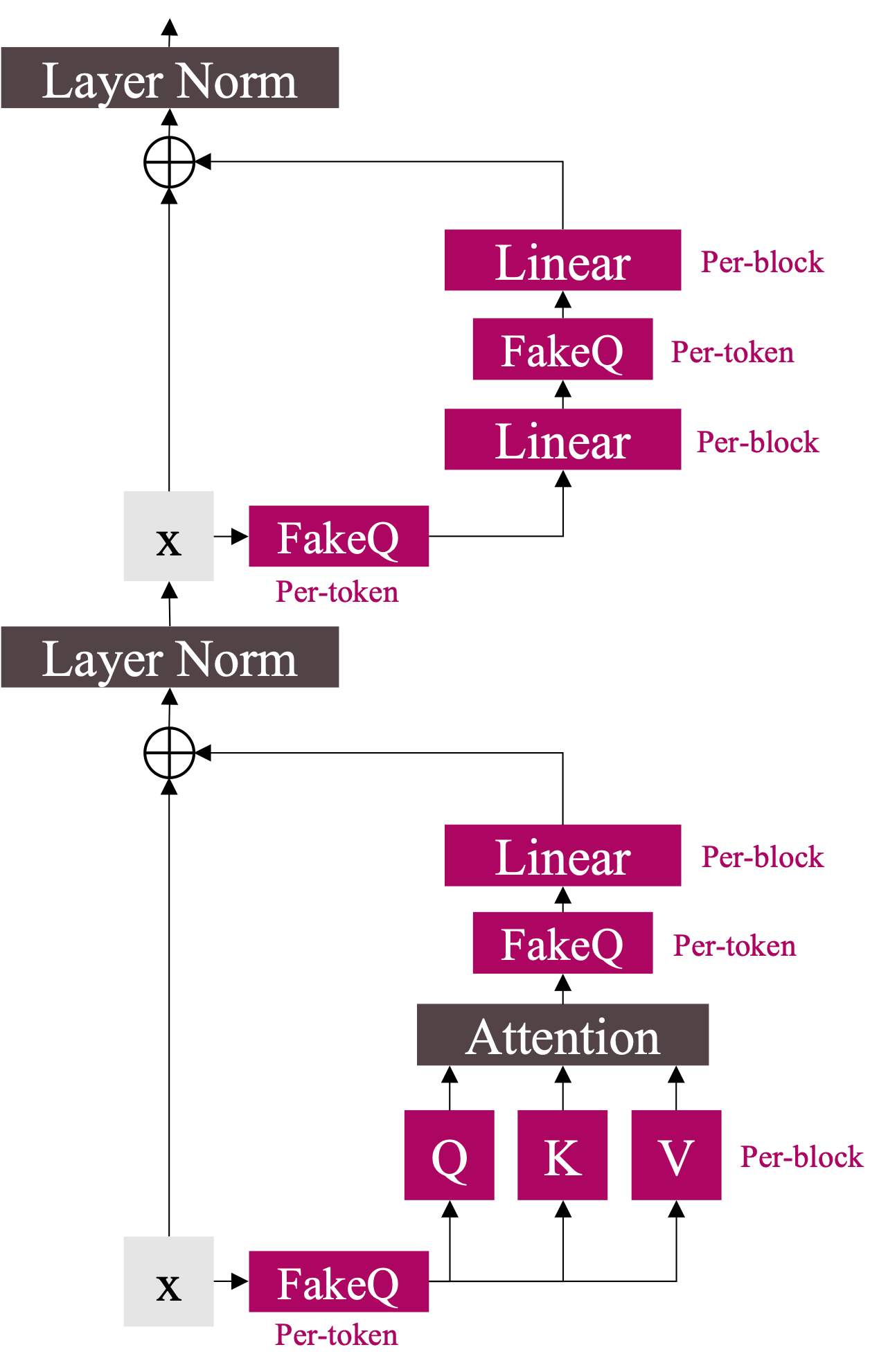
To test this hypothesis, we applied fake quantization during the forward pass (the backward pass is beyond the scope of this posting). Figure 4 illustrates a Transformer model with fake quantization applied. We insert fake quantization blocks into all matrix multiplication operations. Since activation outliers tend to appear in a channel-wise fashion, per-channel quantization is generally preferable. However, to clearly highlight the effects, we applied per-token quantization
While fake quantization does not yield real speedup, it provides a reliable way to evaluate the impact of quantization on model convergence and accuracy.
Experiment Setup
| Hyperparameter | Value |
|---|---|
| max seq length | 128 |
| mlm probability | 0.15 |
| LR rate | 1e-4 |
| LR scheduler | linear |
| max train steps | 1,000,000 |
| warmup steps | 10,000 |
| batch size | 128 |
| gradient accumulation steps | 1 |
| max gradient norm | 1.0 |
| weight decay | 0.01 |
We pre-train all models using the masked language modeling (MLM) objective on Wiki-40b and Bookcorpus datasets, following the BERT-base architecture
Optimization is done by AdamW optimizer with weight decay = 0.01 and a linear learning rate decay schedule, starting from an initial learning rate of 1e-4 with 10K warm-up steps. We train for 1M steps using a batch size of 128 on two A100 GPUs, within max sequence length = 128.
15% of tokens are masked, following the standard BERT masking strategy. All models are trained with FP16
We evaluate six experimental configurations to analyze how gated attention and clipped softmax perform under both FP16 and fake quantized settings. All models use the same architecture and training setup unless otherwise noted:
- Vanilla: Standard model with regular attention and softmax. No FQ.
- Gated Attention (GA): Adds a learnable gating mechanism to attention. No FQ.
- Clipped Softmax (CS): Replaces softmax with a clipped, temperature-scaled version. No FQ.
- Vanilla-FQ: Applies FQ to the baseline model, quantizing weights and activations to 8-bits.
- Gated Attention-FQ (GA-FQ): Combines gated attention with FQ.
- Clipped Softmax-FQ (CS-FQ): Combines clipped softmax with FQ.
Following the prior work’s best hyperparameter setting, we set γ =-0.025 and ζ=1 for clipped softmax, and use MLP with 16 hidden layer for gated attention.
Perplexity Results: Toward Making Training Quantization Work in Practice
| Method | ppl.↓ |
|---|---|
| Vanilla | 5.055 |
| Vanilla-FQ | 542.705 |
| CS | 4.975 |
| GA | 5.004 |
| CS-FQ | 4.994 |
| GA-FQ | 5.301 |
Training quantization applied directly to vanilla BERT results in severe instability, with perplexity exceeding 500, indicating that the model essentially fails to learn altogether. As summarized in Table 2, this catastrophic degradation contrasts sharply with structurally modified variants incorporating outlier mitigation methods such as CS-FQ and GA-FQ. These models consistently maintain low perplexity values around 5.0 and converge stably throughout training.
These results suggest that quantization performance during training can be significantly improved through architectural design, without requiring additional outlier suppression techniques or calibration methods. Overall, our findings highlight that training quantization, while typically fragile, can become a practical and effective optimization strategy when combined with appropriately designed, quantization-friendly architectures.
Training Loss: Outlier Mitigation Enables Stable Training Quantization
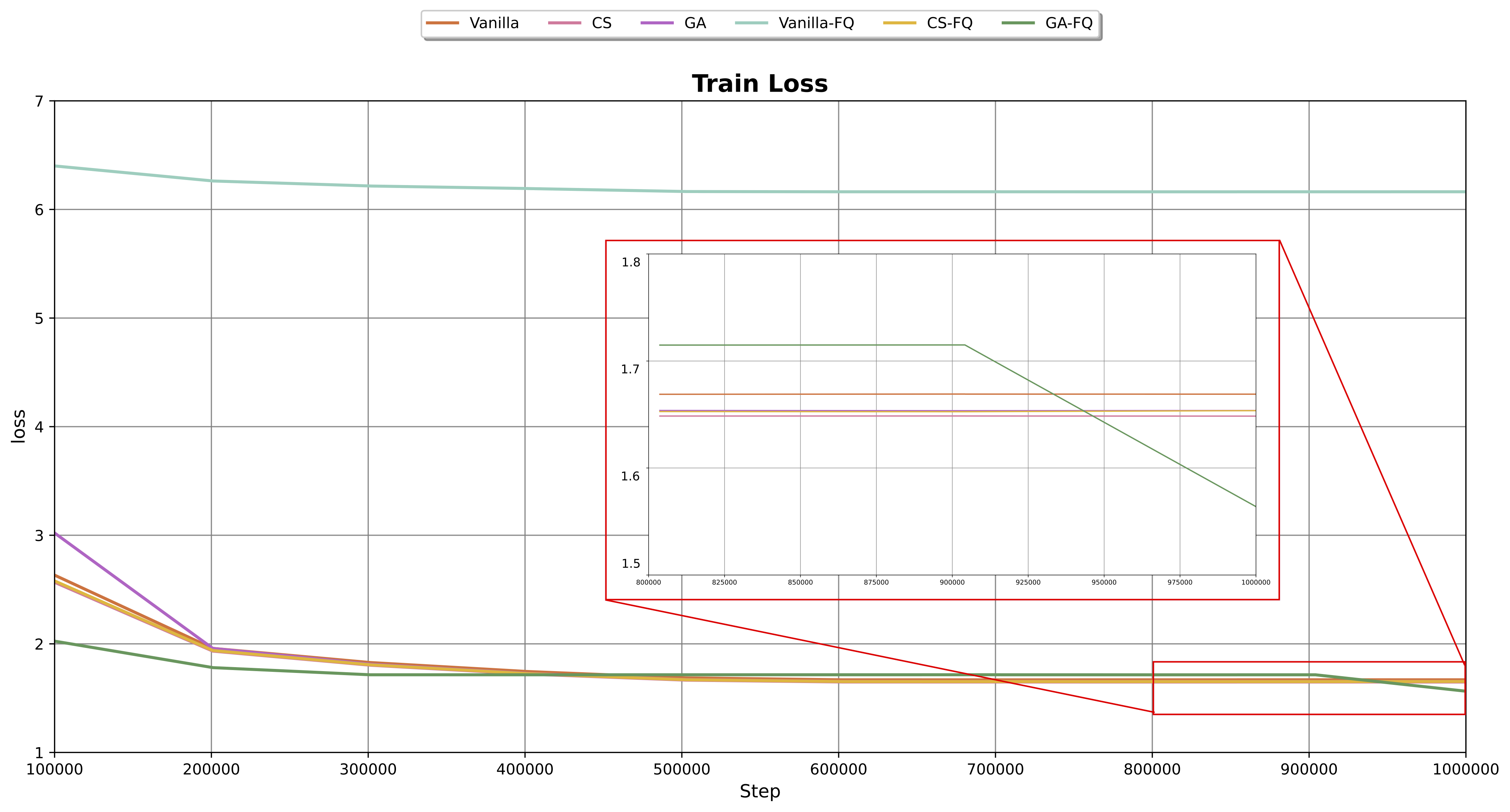
To complement the perplexity analysis, we investigate the training dynamics of each model variant by comparing their training loss values. As showed in Figure 5, vanilla-FQ model results in a significantly higher loss, with an average of 6.16. This indicates poor convergence under quantized training conditions.
In contrast, CS-FQ or GQ-FQ exhibit substantially lower training losses, ranging from 1.65 to 1.71 when trained with quantization, matching with baseline vanilla model. These observations align with the perplexity trends and further support the view that architectural outlier mitigation improves optimization stability in training quantization.
Activation Norm: Outlier Mitigation Enables Quantization Compatibility
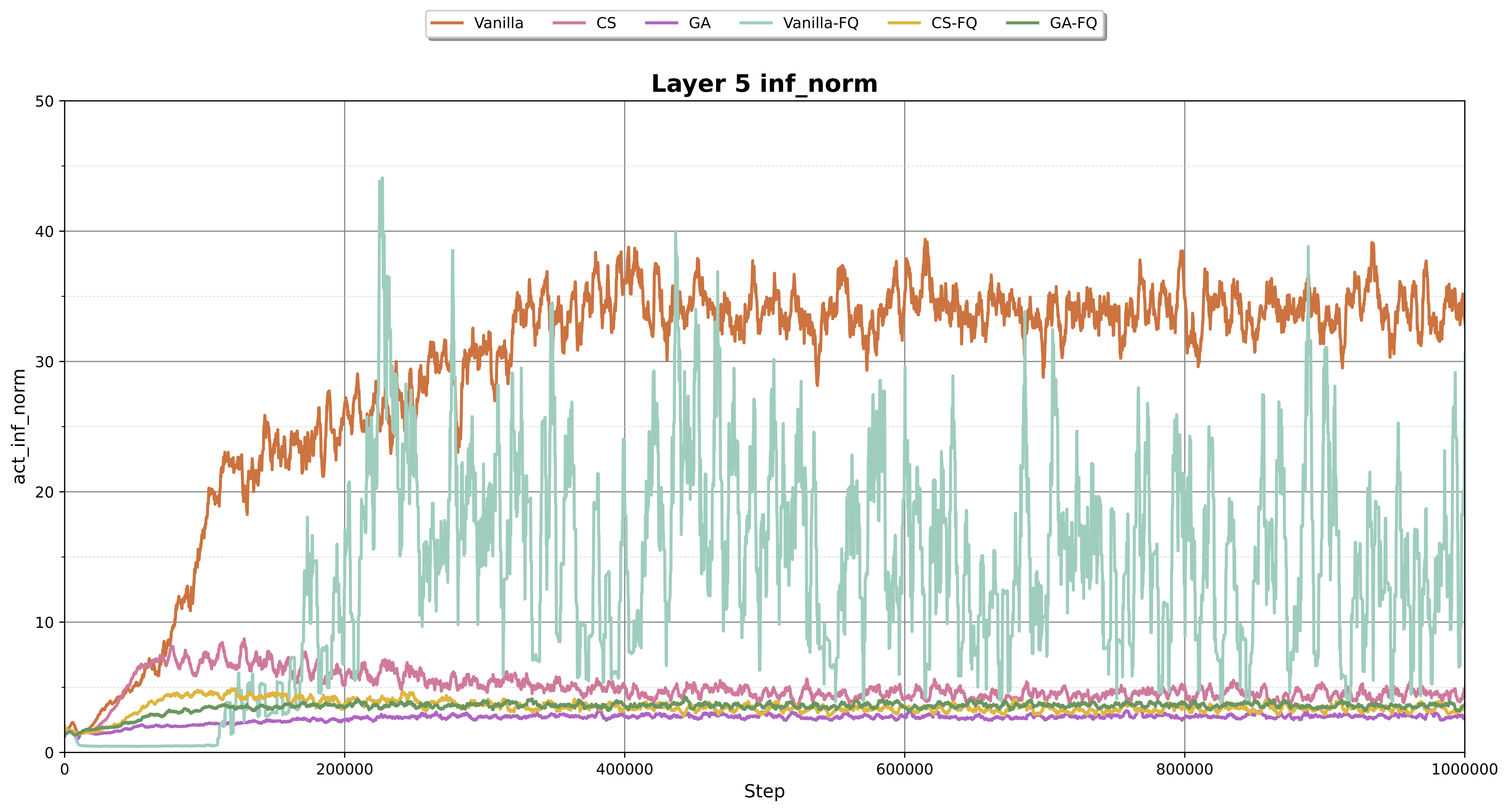
To understand the root cause of the instability observed in vanilla-FQ, we analyze the magnitude of activations in the Transformer block by measuring the \(\|X\|_{\infty}\) of input to model layer. As shown in Figure 6, the baseline vanilla model trained with quantization exhibits extremely high norm values, which are significantly larger than those of any other variant.
In contrast, models incorporating clipped softmax or gated attention produce much lower activation norms. Notably, both CS-FQ and GA-FQ show the low norm matching with CS and GA, presenting substantial norm gap from both the baseline vanilla and vanilla-FQ models. This substantial norm gap between the vanilla-FQ model and the variants with outlier mitigation suggests that mitigating activation outliers is central to stabilizing optimization under training quantization.
Combined with the perplexity and training loss results, this analysis further supports the view that applying outlier mitigation methods forms the foundation for stable and effective training quantization.
Contributions and Limitations of This Work
This work makes two key contributions to the domain of training-time quantization:
- Quantization during the forward pass can be performed without complex outlier suppression techniques, making training-time quantization more accessible.
- Per-token activation quantization introduces minimal quantization error, enabling efficient hardware acceleration.
Several prior works have addressed quantization error during training
However, this work has certain limitations due to the lack of comprehensive experiments and ablations:
- No experiments were conducted with INT4 formats (e.g., W8A4 or W4A4).
- Quantization was only applied to the forward pass; backward pass and gradient outliers were not explored.
As this approach has not been evaluated using INT4 formats, it remains unclear whether it is effective for extremely low-precision training. Moreover, since INT4 quantization is currently not easily accessible due to limited hardware support
Conclusion
In this study, we explored training-time quantization for Transformer models without relying on explicit activation outlier suppression techniques. Our investigation was motivated by the observation that activation outliers—closely linked to the attention sink phenomenon—pose a significant challenge in quantized training. We incorporated clipped softmax and gated sttention, previously shown to reduce activation outliers during training, into the training quantization process. Experimental results demonstrate that the vanilla BERT model suffers severe performance degradation under W8A8 quantization. In contrast, models augmented with either clipped softmax or gated attention maintained comparable performance to their full-precision counterparts in terms of perplexity, training loss, and ∞-norm. These results suggest that simply applying clipped softmax or gated attention is a practical and effective approach to stabilize training under quantization, without the need for additional outlier suppression mechanisms.